What is Numba?

Numba is a just-in-time compiler for Python that translates a subset of Python and NumPy into fast machine code. The most common way to use Numba is through its collection of decorators that can be applied to your functions to instruct Numba to compile them.

When a call is made to a function using the @jit decorator from Numba, it is compiled to machine code “just-in-time” for execution, and part or all of your code can subsequently run at native machine code speed! Numba reads the Python bytecode for a decorated function and combines this with information about the types of the input arguments to the function. It analyzes and optimizes your code, and finally uses the LLVM compiler infrastructure to generate a machine code version of your function, tailored to your CPU capabilities. This compiled version is then used when your function is called.

The Numba @jit decorator fundamentally operates in two compilation modes, nopython mode and object mode. The behaviour of the nopython compilation mode is to essentially compile the decorated function so that it will run entirely without the involvement of the Python interpreter. This is the recommended and best-practice way to use the Numba @jit decorator as it leads to the best performance. It is important to note that nopython mode is not guaranteed to compile successfully. This can happen if there are unsupported functions or classes which are used in the scope of the @jit decorator.

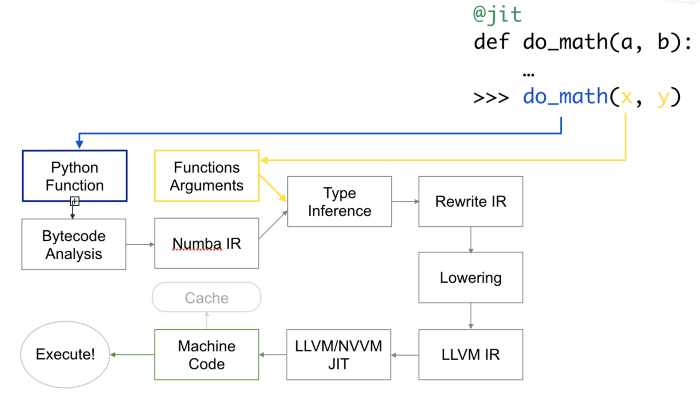
How Numba works. Taken from here.

Increasing support for NumPy functions in Numba

One of the current priorities of Numba is having seamless integration with NumPy. As an intern at Quansight Labs, my main task was extending the list of NumPy functions that are supported by Numba. Since Numba does not understand calls to NumPy functions, developers have to reimplement such functions. The easiest way to do so is using the @numba.extending.overload decorator, which lets the developer write a new implementation of the function in Python. The new implementation needs to have the same behaviour as the original function, but it should also be completely supported by Numba; e.g., it cannot call NumPy functions which are not supported yet. Most importantly, its return type should depend only on the input types and never on the particular values of the inputs.

Numba developers keep track of unsupported NumPy functions in issue #4074. My first task was simple: pick a function from the list and implement it. I started by searching the list for functions that have already been implemented or ones that have been deprecated by NumPy. Then, I decided to pick the function numpy.geomspace, since a very similar function, numpy.logspace, had been implemented already, and this was a great starting point for me. This helped me introduce myself to the Numba development workflow and the repository structure.

After my first pull request was merged, I moved on to other functions from the list. Other NumPy functions for which I added support as a Quansight Labs intern include numpy.vsplit, numpy.hsplit, numpy.dsplit, numpy.rowstack, numpy.diagflat, numpy.resize, numpy.indices and numpy.unwrap. A great guide to using the @overload decorator is given in the Numba documentation.

The NumPy polynomial API

When choosing functions to implement, I was always looking for groups of similar functions. That way, I could get more functions checked off of the list more quickly. This led me to implementing polyadd, polysub, and polymul from numpy.polynomial.polynomial simultaneously.

After seeing this, my mentor asked me if I would like to focus on support for the NumPy polynomial package. I agreed, since I felt like this would be a good way of working with lower levels of Numba. In addition to adding other functions from the polynomial API, the biggest task during my internship was implementing the Polynomial class. It is fairly simple as it has three parameters - coef, domain, and window, each of which is a NumPy array. This meant that the foundation of the implementation was fairly straightforward. Unfortunately, there were a lot of details in the behaviour of the class, and each small detail seemed challenging when I had to implement it using the low-level API. The most interesting thing about the implementation of the class is that the two optional parameters, domain and window, have default values that are NumPy arrays of integer dtype, whereas if the user decides to set domain and window, then these arrays are always cast to arrays of double dtype. This meant that the user could never set the values of these two parameters to their default values. I have opened pull request #24745 in NumPy that aims to improve this behaviour for all classes in the numpy.polynomial package.

Adding support for power series in Numba

Similarly to functions, NumPy classes have to be reimplemented in Numba using its low-level API. A good example of this can be found in the Numba documentation, which I followed very closely. The first big task when working on the Polynomial class was defining a new Numba type to represent the class. After creating a type class called PolynomialType, I needed to "show" Numba that each instance of the Polynomial class should be treated by Numba as if its type is PolynomialType, using the @typeof_impl.register decorator with np.polynomial.polynomial.Polynomial as its argument . Another important part is defining the constructor for the Polynomial class. We decided to add support for Polynomial(coef) and Polynomial(coef, domain, window) at this point. The next step is to define a data model for the new type. That is, how the Polynomial type will be represented in LLVM IR.

The final task when adding support for a new type in Numba is defining special methods for converting Python objects into native values and vice versa. Those operations are called boxing and unboxing. The idea here is that a Python object can be seen as a sophisticated box containing a simple native value which is what the data model needs. The tricky part in my implementation of these two methods was that I had to keep track of whether the domain and window were defined by the user or they were equal to their default values. This part is necessary since the default values of those two parameters can never be set using the constructor, as mentioned above.

Further work on support for NumPy polynomials

Even after my pull requests were merged, there is still a lot of room for further work. For example, NumPy supports five more types of polynomials: Chebyshev series, two types of Hermite series, Laguerre, and Legendre. All of those have the same class structure as the power series, but the behaviour of their methods is different. These differences reflect the different kinds of operations that are being done on them: e.g., the coefficients array of a product of two Chebyshev series is not the same as if we were to multiply Legendre series.

Acknowledgements

I would like to thank Quansight and Christ Church College, Oxford, for providing me the opportunity to work on impactful open source projects in such an amazing environment. I am grateful to my mentor, Guilherme Leobas, for the invaluable support throughout the internship. I would also like to thank Melissa Weber Mendonça for helping me with any general queries as well as sharing her OSS experience during our internship sessions.