What's New in SymPy 1.4
As of November, 2018, I have been working at Quansight, under the heading of Quansight Labs. Quansight Labs is a public-benefit division of Quansight. It provides a home for a "PyData Core Team" which consists of developers, community managers, designers, and documentation writers who build open-source technology and grow open-source communities around all aspects of the AI and Data Science workflow. As a part of this, I am able to spend a fraction of my time working on SymPy. SymPy, for those who do not know, is a symbolic mathematics library written in pure Python. I am the lead maintainer of SymPy.
SymPy 1.4 was released on April 9, 2019. In this post, I'd like to go over some of the highlights for this release. The full release notes for the release can be found on the SymPy wiki.
To update to SymPy 1.4, use
conda install sympy
or if you prefer to use pip
pip install -U sympy
The SymPy 1.4 release contains over 500 changes from 38 different submodules, so I will not be going over every change, but only a few of the main highlights. A total of 104 people contributed to this release, of whom 66 contributed for the first time for this release.
While I did not personally work on any of the changes listed below (my work for this release tended to be more invisible, behind the scenes fixes), I did do the release itself.
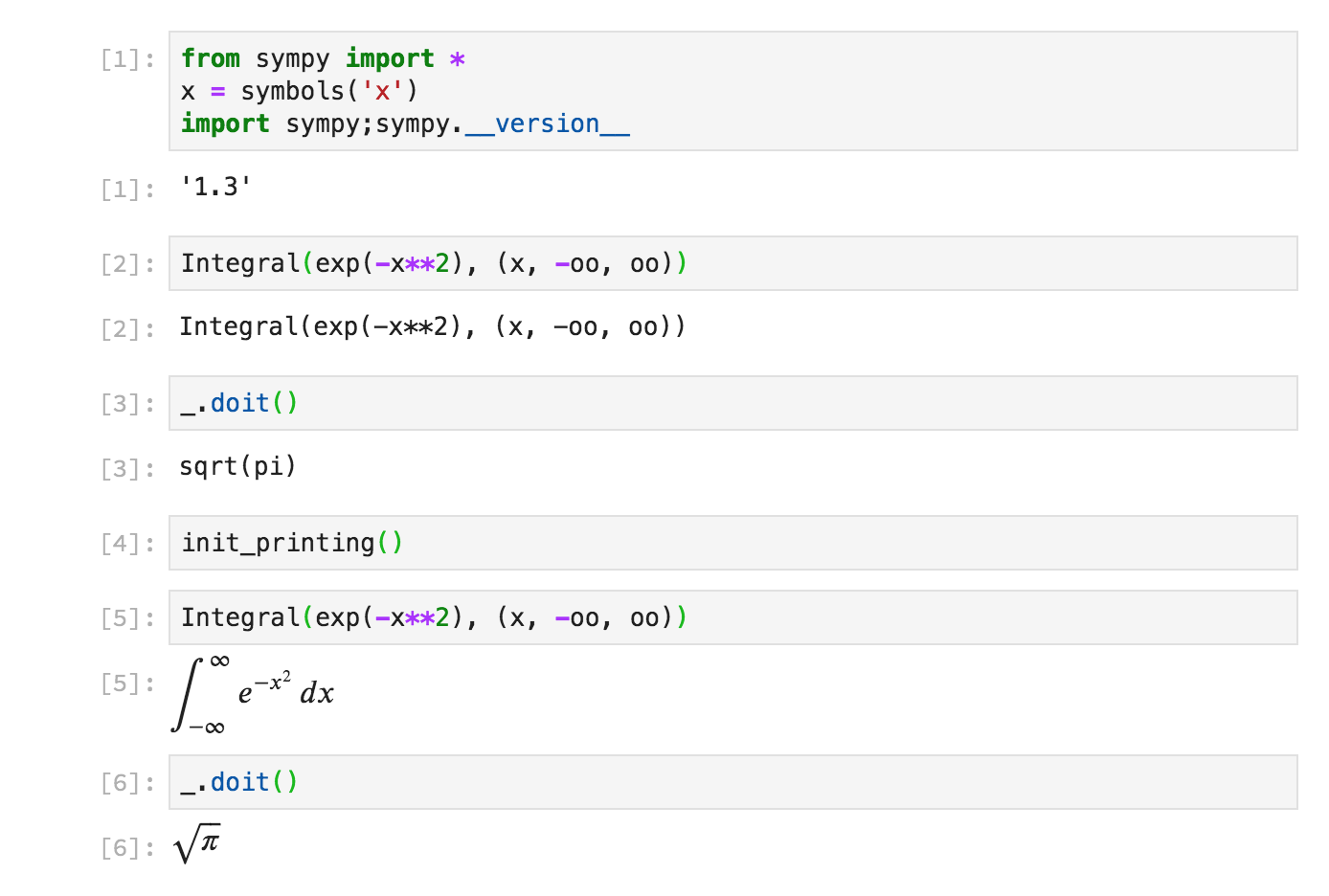
Automatic LaTeX rendering in the Jupyter notebook
Prior to SymPy 1.4, SymPy expressions in the notebook rendered by default with their
string representation. To get LaTeX output, you had to call init_printing():
In SymPy 1.4, SymPy expressions now automatically render as LaTeX in the notebook:
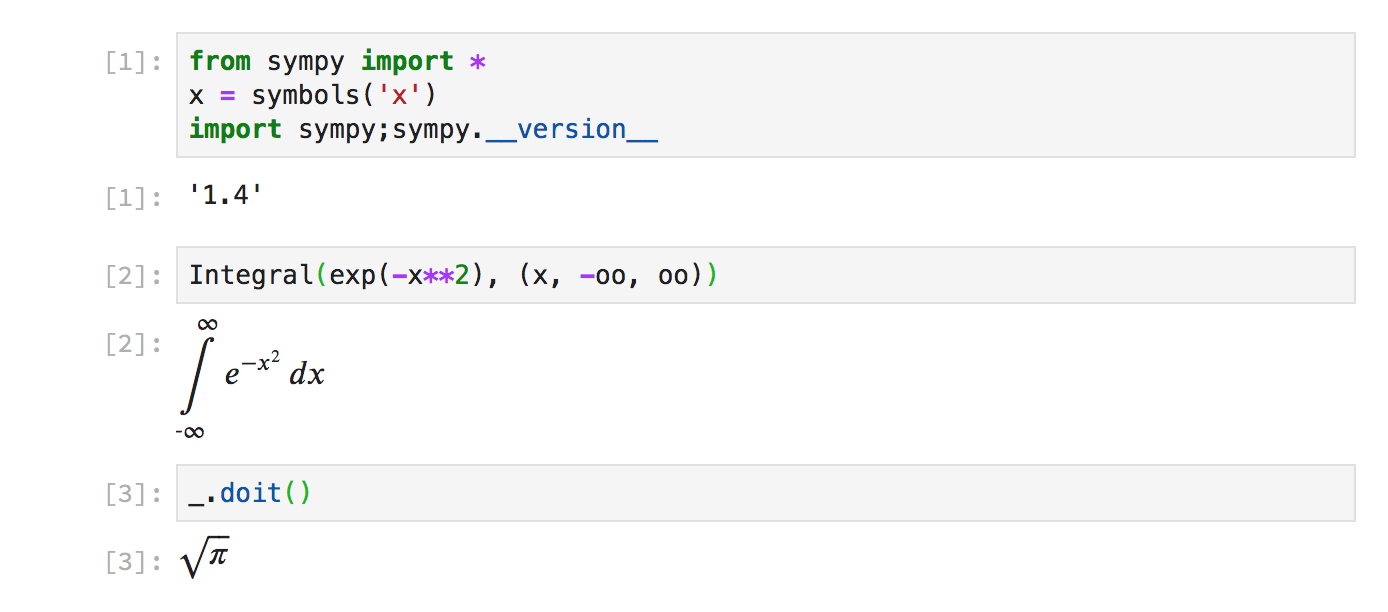
However, this only applies automatically if the type of an object is a SymPy
expression. For built-in types such as lists or ints, init_printing() is
still required to get LaTeX printing. For example, solve() returns a list,
so does not render as LaTeX unless init_printing() is called:
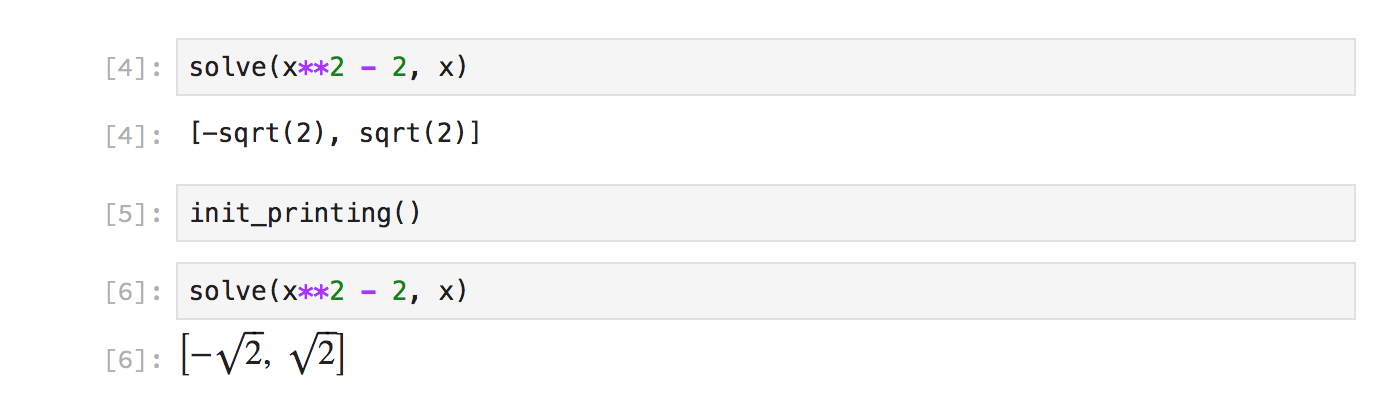
init_printing() is also still needed if you want to change any of the
printing settings, for instance, passing flags to the latex() printer or
selecting a different printer.
If you want the string form of an expression for copy-pasting, you can use
print.
Improved simplification of relational expressions
Simplification of relational and piecewise expressions has been improved:
>>> x, y, z, w = symbols('x y z w')
>>> init_printing()
>>> expr = And(Eq(x,y), x >= y, w < y, y >= z, z < y)
>>> expr
x = y ∧ x ≥ y ∧ y ≥ z ∧ w < y ∧ z < y
>>> simplify(expr)
x = y ∧ y > Max(w, z)
>>> expr = Piecewise((x*y, And(x >= y, Eq(y, 0))), (x - 1, Eq(x, 1)), (0, True))
>>> expr
⎧ x⋅y for y = 0 ∧ x ≥ y
⎪
⎨x - 1 for x = 1
⎪
⎩ 0 otherwise
>>> simplify(expr)
0
Improved MathML printing
The MathML presentation printer has been greatly improved, putting it on par with the existing Unicode and LaTeX pretty printers.
>>> mathml(Integral(exp(-x**2), (x, -oo, oo)), 'presentation')
<mrow><msubsup><mo>∫</mo><mrow><mo>-</mo><mi>∞</mi></mrow><mi>∞</mi></msubsup><msup><mi>ⅇ</mi><mrow><mo>-</mo><msup><mi>x</mi><mn>2</mn></msup></mrow></msup><mo>ⅆ</mo><mi>x</mi></mrow>
If your browser supports MathML (at the
time of writing, only Firefox and Safari), you should see the above
presentation form for Integral(exp(-x**2), (x, -oo, oo)) below:
Improvements to solvers
Several improvements have been made to the solvers.
>>> eq = Eq((x**2 - 7*x + 11)**(x**2 - 13*x + 42), 1)
>>> eq
2
x - 13⋅x + 42
⎛ 2 ⎞
⎝x - 7⋅x + 11⎠ = 1
>>> solve(eq, x) # In SymPy 1.3, this only gave the partial solution [2, 5, 6, 7]
[2, 3, 4, 5, 6, 7]
The ODE solver, dsolve, has also seen some improvements. Two new hints have
been added.
'nth_algebraic' solves ODEs using solve by inverting the derivatives
algebraically:
>>> f = Function('f')
>>> eq = Eq(f(x) * (f(x).diff(x)**2 - 1), 0)
>>> eq
⎛ 2 ⎞
⎜⎛d ⎞ ⎟
⎜⎜──(f(x))⎟ - 1⎟⋅f(x) = 0
⎝⎝dx ⎠ ⎠
>>> dsolve(eq, f(x)) # In SymPy 1.3, this only gave the solution f(x) = C1 - x
[f(x) = 0, f(x) = C₁ - x, f(x) = C₁ + x]
'nth_order_reducible' solves ODEs that only involve derivatives of f(x),
via the substitution g(x)=f(n)(x).
>>> eq = Eq(Derivative(f(x), (x, 2)) + x*Derivative(f(x), x), x)
>>> eq
2
d d
x⋅──(f(x)) + ───(f(x)) = x
dx 2
dx
>>> dsolve(eq, f(x))
⎛√2⋅x⎞
f(x) = C₁ + C₂⋅erf⎜────⎟ + x
⎝ 2 ⎠
Dropping Python 3.4 support
This is the last release of SymPy to support Python 3.4. SymPy 1.4 supports Python 2.7, 3.4, 3.5, 3.6, 3.7, and PyPy. What's perhaps more exciting is that the next release of SymPy, 1.5, which will be released later this year, will be the last version to support Python 2.7.
Our policy is to drop support for major Python versions when they reach their End of Life. In other words, they receive no further support from the core Python team. Python 3.4 reached its end of life on May 19 of this year, and Python 2.7 will reach its end of life on January 1, 2020.
I have blogged in the past on why I believe it is important for library authors to be proactive in dropping Python 2 support, and since then a large number of Python libraries have either dropped support or announced their plans to by 2020.
Having Python 2 support removed will not only allow us to remove a large amount of compatibility cruft from our codebase, it will also allow us to use some Python 3-only features that will clean up our API, such as keyword-only arguments, type hints, and Unicode variable names. It will also enable several internal changes that will not be visible to end-users, but which will result in a much cleaner and more maintainable codebase.
If you are still using Python 2, I strongly recommend switching to Python 3,
as otherwise the entire ecosystem of Python libraries is soon going to stop
improving for you. Python 3 is already highly recommended for SymPy usage due
to several key improvements. In particular, in Python 3, division of two
Python ints like 1/2 produces the float 0.5. In Python 2, it does
integer division (producing 1/2 == 0). The Python 2 integer division
behavior can lead to very surprising results when using SymPy (imagine writing
x**2 + 1/2*x + 2 and having the x term "disappear"). When using SymPy, we
recommend
using rational numbers (like Rational(1, 2)) and avoiding int/int, but the
Python 3 behavior will at least maintain a mathematically correct result if
you do not do this. SymPy is also already faster in Python
3
due to things like math.gcd and functools.lru_cache being written in C,
and general performance improvements in the interpreter itself.
And much more
These are only a few of the highlights of the hundreds of changes in this release. The full release notes can be found on our wiki. The wiki also has the in progress changes for our next release, SymPy 1.5, which will be released later this year. Our bot automatically collects release notes from every pull request, meaning SymPy releases have very comprehensive and readable release notes pages. If you see any mistakes on either page, feel free to edit the wiki and fix them.
Comments